The missing grandchildren of Argentina are a well-known collection of missing person cases. From 1976 to 1983, Argentina suffered a military civic dictatorship. It is estimated that 30,000 people were kidnapped, sent to clandestine centers, tortured and murdered. Most of them are still missing.
Many women were pregnant at the time of abduction. Rapes were also common, frequently resulting in pregnancies. Children kidnapped with their parents or born in captivity were killed or delivered to families related to, or from, the military forces as “war booty”, and their identities were forged. In most cases their biological parents were murdered, and their bodies still remain missing.
As the regime eventually ended by 1983, grandmothers of the abducted children (organized in the association Abuelas de Plaza de Mayo) started to enquire the scientific community and the new democratic government to aid them in the search for their missing grandchildren.
Written by: Mariana Herrera Piñero, Banco Nacional de Datos Genéticos
In 1987, the Banco Nacional de Datos Genéticos (BNDG) was created through the passing of specific laws. Since then, the BNDG has collected DNA from relatives (mainly grandparents, uncles/aunts and siblings) of appropriated children, and performed genetic analyses on thousands of children suspected to be one of the missing grandchildren.
As of March, 2017, such DNA analyses have contributed to the identification of 75 children. The BNDG has also assisted children born after abduction, through the aid of DNA studies, to register them with the surname of their true family.
Most of the family groups represented in our DNA database lack the genetic information of the missing children’s parents. Many of them have few relatives (grandparents, uncles or brothers from the missing grandchild).
The main question is whether or not these incomplete family groups have sufficient statistical power to correctly identify the biological missing grandchild in case it comes to the National Genetic Databank.
Methods and implementations of DNA-based identification are well established in several forensic contexts. However, assessing the statistical power of these methods has been largely overlooked, except in the simplest cases.
In our presentation, we outlined general methods for such power evaluation, and applied them to a large set of family reunification cases, where the objective is to decide whether a person of interest (POI) is identical to the missing person (MP) in a family, based on the DNA profile of the POI and available family members. As such, this application closely resembles database searching and disaster victim identification (DVI).
If parents or children of the MP are available, they will typically provide sufficient statistical evidence to settle the case. However, if one must resort to more distant relatives, it is not a priori obvious that a reliable conclusion is likely to be reached. In these cases, power evaluation can be highly valuable, for instance in the recruitment of additional family members.
You may also like:
The Study
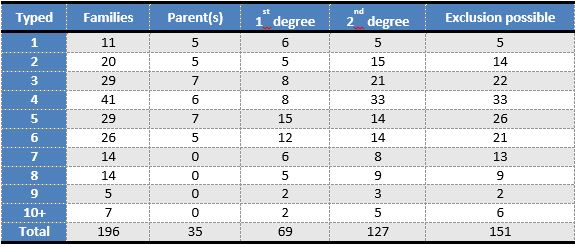
This study covers 196 of those reference families. The task is to determine whether a given person of interest (POI) is identical to the missing person (MP) of a given family. In the present study only families with a single missing member are considered, but the methods and implementation can account for extended scenarios, involving several missing persons in the same family.
Summary statistics of all 196 reference families included in this study are given in the table below, providing an overview of the number of typed relatives and their relationship to the missing person.
For a given person of interest we consider the following hypotheses:
H1: POI is MP
H2: POI is unrelated to MP
After genotyping the POI together with one or more family members, a statistical comparison of the above hypotheses is typically done using the likelihood ratio (LR). In this study we use two measures to determine the statistical power for each family:
- Exclusion probability (PE) – The probability that an unrelated person will be excluded as the MP. In other words, given that H2 is true, how likely is it to observe genetic inconsistencies.
- Exceedance probability (Et) – The probability that the LR will exceed a certain threshold. In other words, given that H1 is true, how likely is it to exceed a threshold t.
To find these statistics we use conditional simulations. In contrast to unconditional simulations, conditional simulations use the genotype data from typed family members to find the LR distributions. Generally, the former provides an idea of the power for any family with the given relatives and number of markers, whereas the latter provides an idea of the power to identify for each unique family.
We provide an implementation in the latest version of the freely available software Familias available at http://www.familias.no, making use of the R library paramlink.
The conditional procedure is highly computer intensive due to the many likelihood computations necessary. To overcome this, we provided an implementation in the latest version Familias [2, 3], making use of the R library paramlink [4]. The R-package paramlink implements several speedups, combining different simulation strategies in order to minimize the number of likelihood computations. These strategies include computing joint genotype distributions for selected individuals and gene dropping where this is possible.
We performed conditional simulations on all unsolved cases – in total 171 – in our selection of 196 reference families from the BNDG database.
Key Collaborators
- Daniel Kling : Department of Forensic Services, Oslo University Hospital Oslo, Norway
- Thore Egeland : IKBM, Norwegian University of Life Sciences, Ås, Norway
- Magnus Dehli Vigeland : Department of Medical Genetics, Oslo University Hospital, Oslo, Norway
Results
We got the exclusion probability PE and the estimated exceedance probability E10000 = P(LR>10,000 | H1) for each family. As expected, cases with a high exclusion probability also tend to have a high exceedance probability, as both statistics increase with the amount of genetic data available.
In total, 58 families (one third of those investigated) have E10000 < 0.8, indicating low power and the necessity for additional genetic data. In contrast, 68 families have both E10000 and PE greater than 0.99, indicating excellent statistical power both for positive matching and exclusion. Included among these are all cases where parental data is available, except one case where few markers were typed. The remaining 45 families have decent power for positive identification, with 0.8 < E10000 < 0.99. Most of these also have high PE, with a few exceptions where the particular configuration of typed relatives make exclusion theoretically impossible.
A majority of the BNDG reference families lack first-degree relatives of the missing person. For example, parental data was available in only 35 of the 196 families included in this study. This makes accurate power assessment an essential tool when recruiting family members.
This work caught the attention of many professionals that work in Disaster Victim Identification who are interested in creating reference family databases and insuring the genetic data is enough to make a positive identification in these kind of searches.
This work will also set the basis for applying criteria for the decision of analyzing maternal and paternal lineages in those families that the exclusion probability and the exceedance probability are low.
We are currently completing the reference families with more relatives. Many of them have to be exhumed because they passed away before giving a sample to the Bank. We are also increasing the number of autosomal markers analyzed, and comparing the current simulations with the upcoming results. We have started to run conditional simulations as a routine in each new family group that arrives to our Databank.
Would you like to see more articles like this? Subscribe to the ISHI blog below!
Subscribe Now!